Secuencia didáctica
para la enseñanza de la geometría a través del método
problémico en educación básica
Didactic
sequence for the teaching of geometry through the problem
method in basic
education
Recibido: 16
de diciembre 2020,
Evaluado: 12
de febrero 2021,
Aceptado: 10
de abril 2021
Rolando Oscco Solorzano
https://orcid.org/0000-0001-9610-5912
Universidad Nacional de
Educación “Enrique Guzmán y Valle”
Richard Santiago Quivio Cuno
https://orcid.org/0000-0002-5986-3711
Universidad Nacional de
Educación “Enrique Guzmán y Valle”
DOI: https://doi.org/10.35756/educaumch.202117.184
Como citar
Oscco
Solorzano, R., & Quivio Cuno, R. (2021). Secuencia didáctica para la
enseñanza de la geometría a través del método problémico en educación
básica. Revista EDUCA UMCH, (17), 173-187 https://doi.org/10.35756/educaumch.202117.184
Resumen
El artículo
que se presenta tiene por objetivo mostrar algunas orientaciones concretas sobre la aplicación de métodos problémicos
dentro de las estrategias didácticas para perfeccionar los procesos de enseñanza-aprendizaje de la Geometría en los
estudiantes de Educación Básica. El método aplicado
para este artículo
se apoyó en revisiones de carácter documental, para lo que se tuvo en cuenta que este tipo de enseñanza se adhiere al constructivismo
como paradigma educativo. Esta propuesta metodológica está orientada a guiar al docente
en su práctica pedagógica y, por ende, al logro de las competencias necesarias en los estudiantes, como lo exige hoy el currículo nacional de
carácter constructivista. Por lo tanto,
dentro de las conclusiones más importantes presenta una perspectiva formativa
sólida en cuanto a la aplicación de
los referidos métodos como alternativa metodológica concreta a través
de diferentes ejemplos
brindados.
Palabras claves:
método problémico, constructivismo y enseñanza de la geometría
Summary
The
article that is presented aims to show some specific guidelines on the
application of problem methods within the didactic strategies to improve the
teaching-learning processes of Geometry in students of Basic Education. The
method applied for this article was supported by documentary reviews, for which
it was taken into account that this type of teaching adheres to constructivism
as an educational paradigm. This methodological proposal is aimed at guiding
the teacher in their pedagogical practice and, therefore, at the achievement of
the necessary competencies in students, as required today by the national
constructivist curriculum. Therefore, among the most important conclusions, it
presents a solid formative perspective regarding the application of the aforementioned
methods as a concrete methodological alternative through different examples
provided.
Keywords:
problem method, constructivism and teaching of geometry
Introducción
Se ha hecho evidente en estos momentos, que el proceso de enseñanza-aprendizaje, debe marchar de acuerdo al desarrollo social en general que crece con ritmo vertiginoso. Lo contrario sería caer en un antagonismo que relega a la educación respecto a estos cambios sociales.
Debido a esto, en las últimas décadas se están poniendo en práctica modelos de aprendizaje que responden a estos cambios, ya que los esquemas pedagógicos tradicionales vienen resultando no funcionales. En ellos, al estudiante apenas se le daba protagonismo y solo se aplicaba la relación sujeto-objeto durante el proceso enseñanza-aprendizaje. Es por lo anterior que en los últimos tiempos se están aplicando metodologías activas, enfocadas al acto de aprender, donde al estudiante también le corresponden papeles activos en este proceso, y junto al profesor, se convierte en actor del mismo.
Desde Piaget1 y Vygotsky2 hasta la actualidad, han surgido variantes de los métodos basados en el constructivismo, pero la realidad ha demostrado que ponerlos en la práctica no ha resultado tan sencillo como algunos presuponen; sobre todo en países que no han podido desprenderse del tradicional conductismo.
A juicio de los autores, hay tres causas esenciales de la anterior consecuencia, una de ellas es la lógica oposición al cambio que surge en todas las esferas de la vida cuando hay formas y hábitos arraigados en el entorno escolar, incluyendo por supuesto a los profesores. La otra corresponde, al menos en el Perú, a la preparación, actualización y capacitación de los docentes para enfrentarse a un nuevo sistema que conlleva al cambio de estrategias metodológicas, objetivos y evaluación, entre otras; y la tercera, pero no menos importante, a la respuesta de los estudiantes para lograr el éxito en los conocimientos, habilidades y capacidades que se espera de los métodos activos teniendo en cuenta que se han adaptado a los discursos tradicionales.
Desde luego, cuando nos referimos a métodos activos, estamos destacando aquellos que le dan participación directa al estudiante durante el proceso enseñanza- aprendizaje y no lo convierten en un ente pasivo como ocurría con los métodos conductistas.
Por lo expuesto, hoy se habla y a la vez se ponen en práctica otros sistemas que responden a estos métodos activos, como el método de descubrimiento guiado, el llamado método dialéctico, el método lúdico, el método socializado, etc.
Aunque, en este artículo se enfatizará en el método problémico o enseñanza por problemas, como una metodología de enseñanza-aprendizaje, aplicada específicamente al aprendizaje de la geometría a través de ejemplos prácticos.
Lo problémico en la enseñanza y en el aprendizaje
La aplicación de los métodos en los procesos de enseñanza-aprendizaje cobran importancia y son vías para el logro de los objetivos. En este sentido, el rol del docente está en escoger y aplicar métodos pertinentes que ayuden a los estudiantes a construir sus propios aprendizajes. En la literatura científica consultada, aparecen diversidad de métodos, al margen del método que se adopte, va a depender de la capacidad y creatividad del docente de poder combinar los componentes en los procesos de enseñanza-aprendizaje. Uno de estos métodos es el problémico o la enseñanza problémica. Al respecto Majmutov (1983); García (2015); Montejo (2016); Reyes, Carrillo y Caamaño (2017) y Cabrera, Álvarez y Marrero (2018), sostienen que el método problémico representa una forma de enseñanza cuya esencia consiste en que la asimilación de los conocimientos no solo se puede dar por la apropiación de las reglas, leyes y teorías que brinda el docente, sino mediante la elaboración lógica del propio estudiante: es una actividad independiente donde no solo se desarrolla la memoria, sino las capacidades de pensamiento.
En términos de Reyes, Carrillo y Caamaño (2017), la metodología de enseñanza problémica propicia un aprendizaje autorregulado, reflexivo, critico, intencional y consiente.
De
igual modo, Ortiz (2015), plantea que “la enseñanza problémica como pilar
pedagógico desempeña un papel fundamental en la formación de la independencia cognoscitiva y el desarrollo
las capacidades creadoras de los estudiantes, al promover el desarrollo de la capacidad autónoma, creadora
y el constante auto mejoramiento del individuo” (p. 100).
Cabe resaltar que, en esta metodología, el estudiante se introduce en la búsqueda de la solución de nuevos problemas con el apoyo del docente, lo cual permite adquirir independientemente los conocimientos con el dominio de la actividad creadora. De esta manera se desarrolla el pensamiento creador, que es la función primordial de la enseñanza problémica.
Uno de los precursores de este tipo de enseñanza fue el ruso Majmutov (1983), quien la definió como “la actividad durante el proceso docente educativo donde se crean situaciones por parte del docente con el planteamiento de problemas que debe resolver el estudiante por sí solo en la asimilación de conocimientos nuevos” (p. 34). ¿Pero a qué llamó problema? Al respecto puede haber varias definiciones, pero casi todas coincidentes cuando se plantea que un problema es algo desconocido que desea saber el estudiante, pero debe estar en condiciones, en sus operaciones mentales para conocerlo.
Aunque mucho antes, otros pedagogos sentaron las bases para este tipo de enseñanza. A continuación, brindamos un breve comentario tomado de la revista cubana Humanidades Médicas, escrito por Azcuy, Nápoles, Infante, Rivero y Ramírez (2004) respectivamente, cuando plantean: La enseñanza problémica no surge en
la actualidad, sus raíces provienen de los primeros intentos por enseñar a pensar desde siglos anteriores. Sócrates utilizó con sus pupilos un método al que él denominó Mayéutica, en el que está presente la activación de los estudiantes en el proceso docente educativo. En el decurso del tiempo, otros pedagogos continuaron esta práctica. Así, el gran pedagogo y padre de la pedagogía Jan Amos Comenius planteó en sus obras la preocupación por la utilización de un método que provocara en el estudiante cierto grado de problemicidad. También, el pedagogo suizo Juan Enrique Pestalozzi en cuya obra se encaminó a activar el proceso de enseñanza mediante la observación, generalización y las conclusiones personales para desarrollar el pensamiento.
Según Majmutov (1983) el problema y las operaciones mentales del estudiante deben transitar por etapas. Específicamente el propio pedagogo ruso subraya la creación de contradicciones en el estudiante para crear en él una necesidad de buscar soluciones. Lo anterior puede esquematizarse de la forma siguiente:
Dicho de otra forma y considerando al acto de enseñar y aprender como parte de la investigación científica, las etapas por las que va transitando el estudiante en su aprendizaje van en orden ascendente, y es el docente quien debe crear las condiciones para ello.
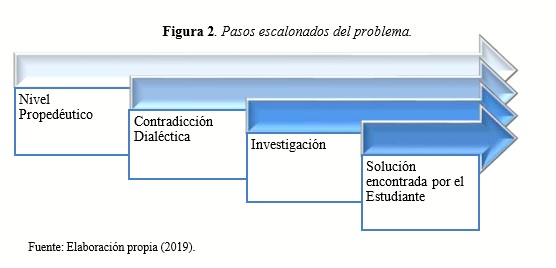
En el esquema anterior se hace evidente que todos los pasos descansan en el nivel propedéutico o preparatorio, donde se posee la base cognitiva necesaria de los conocimientos precedentes.
En resumen, las exigencias de las situaciones problémicas requieren: a). Crear una dificultad en el estudiante (Problema). b). Procurar que ella genere una necesidad de búsqueda. c). Impulsar a descubrir lo desconocido a partir de elementos conocidos. Abundando en lo anterior, cuando se plantea crear una dificultad, esto se enfoca de acuerdo con sus operaciones mentales. Es como crear la duda que motiva a descubrir lo que no conoce, por tanto, no es una dificultad antagónica, que tiene su significación en el problema en sí como hemos planteado en la necesidad de búsqueda (motivación), aclarando que motivación no es lo mismo que curiosidad, ya que la curiosidad desaparece cuando descubrimos algo que no conocemos y así el interés por lo desconocido, mientras que la motivación sigue una cadena lógica que impulsa a seguir indagando. El último aspecto referido, también guarda una estrecha relación con los anteriores, ya que para aprender lo nuevo se necesita una base precedente como hemos explicado con anterioridad.
Métodos o variantes propuestas en la enseñanza problémica
Hay autores que han buscado alternativas al aplicar este tipo de enseñanza en el aula. Para ello se han apoyado en los elementos teóricos que conllevan a un aprendizaje activo en los estudiantes, según las condiciones de cada contexto y de cada clase. En términos de Reyes, Carrillo y Caamaño (2017), existen ciertas categorías que se manifiestan en el desarrollo del método problémico, estas son la exposición problémica, la conversación heurística, la búsqueda parcial y el método investigativo. A continuación, detallamos los procesos didácticos para seguir en la aplicación del método problémico, mediante la aplicación de las cuatro categorías mencionadas.
La exposición problémica
El docente va revelando gradualmente lo fundamental del conocimiento, pero no de forma acabada. Este método es muy usado a veces empíricamente en el que se le induce al estudiante parte del problema para que él llegue por sí solo a su solución final.
Profundizando más en este aspecto, hay que enfatizar en el papel del docente como guía y él lo debe tener muy en cuenta durante su preparación para no plantear el problema y dar su solución acabada. Durante la planificación de su clase, debe concebirla de forma escalonada cumpliendo el principio didáctico de asequibilidad, es decir, ofrecer las bases cognitivas que conlleven al estudiante a buscar la solución del problema.
Podemos citar un caso de geometría m u y sencillo, pero dividido en dos partes: Por ejemplo: demuestra que, en un triángulo, la suma de todos los ángulos es de 180°
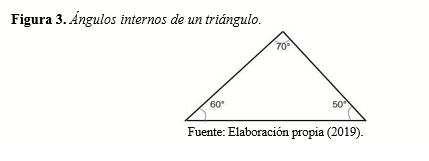
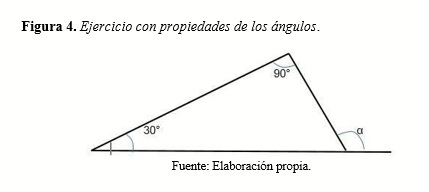
Las características de la exposición problémica pueden resumirse en lo siguiente: a). La exposición es demostrativa (comprobable). b). Contribuye al desarrollo paulatino del pensamiento científico. c). Despierta la motivación y aumenta el interés de participación bajo un ambiente de libertad de acción.
a. La conversación heurística
Es el método más antiguo. El docente activa la actuación cognoscitiva de los estudiantes a través del debate, donde propicia una cadena de razonamientos e interrogantes, al utilizar los conocimientos antecedentes.
Otro ejemplo, que utiliza la geometría acerca de este método, lo puede propiciar el docente a través de la siguiente pregunta: ¿La distancia real entre el Ecuador y el polo norte puede proporcionarla un mapa?
Aquí el estudiante está listo para el debate en colectivo cuando el docente se auxilia primero de un mapa y luego de un globo terráqueo. Es evidente que un mapa plano no ofrece curvatura y de momento, el estudiante tratará de dibujar una recta, pero cuando enseñe el globo terráqueo, se dará cuenta de que la recta no es la solución.
Son varias las ventajas de este tipo de método, ya que el estudiante aprende a escuchar las opiniones de sus compañeros, enseña a aceptar y discutir criterios, acepta las equivocaciones y se expresa sin temor.
En la conversación heurística es fundamental el papel de guía del docente para su correcta moderación.
b. Búsqueda parcial
En la búsqueda parcial, el docente orienta algún tipo de tarea investigativa como parte de un tema cualquiera. Ese es un trabajo investigativo dentro de un estudio general y se usa en todas las asignaturas.
Es conveniente auxiliarse de medios de enseñanza convenientemente planificados para que el estudiante manipule y bajo la orientación del profesor, llegue a la respuesta.
Por ejemplo, se les reparte a los estudiantes la cuarta parte de una esfera maciza de madera o cualquier material y se les propone calcular el volumen de esa cuarta parte de la esfera.
Se
recomienda que cada objeto sea
diferente y se les entrega una regla milimétrica. El antecedente en este caso radica en
que conozcan de antemano
la fórmula del volumen de la
esfera: V= 4/3. π R3.
Esto es aplicable a todas las asignaturas, previa planificación del docente.
c. El método investigativo
Es un tipo de método científico que acerca a los estudiantes a la indagación y observación de hechos naturales o sociales. Se caracteriza por su gran independencia cognoscitiva y el aumento de la actividad creadora. En este caso, la función del docente consiste en su control y revisión; y familiariza al estudiante con la investigación científica.
Por ser algo más complejo que los anteriores, se usa frecuentemente en tareas para la casa o fuera del horario docente. También es primordial la certera planificación del docente quien debe estar atento a la secuencia de conocimientos precedentes, ya que, si hay algún salto entre ellos, entonces no se lograrán los objetivos que se persiguen.
Una aplicable sugerencia para modelar la geometría del espacio
En este trabajo, proponemos aplicar la Enseñanza Problémica como un método sencillo donde se utilicen materiales de fácil adquisición. Para ello escogemos la geometría del espacio porque en ella normalmente se visualiza poco cuando la tratamos de enseñar con imágenes planas, ya que como sabemos, nuestra representación mental está condicionada en dos dimensiones, y al representar objetos en una pizarra, vemos la televisión, o leemos, lo hacemos de esa forma. Trabajar en dos dimensiones siempre ha resuelto nuestros problemas de las representaciones visuales, pero no nos ofrece una información completa de nuestro objeto de estudio.
Sin embargo, cuando condicionamos nuestra representación de la realidad objetiva de forma estereométrica, entonces aumenta considerablemente el nivel de información.
Por ejemplo, en las fábricas de aviones, luego del plano, se construye un modelo sólido pequeño de la futura nave, para analizar y medir sus condiciones aerodinámicas. Igual ocurre con los modelos de automóviles y las maquetas de edificios. En estos casos, los objetos sirven de patrones a pequeña escala, para luego convertirlos en la realidad. Para ello se toman tanto las características cualitativas como cuantitativas del objeto prueba.
También hay sistemas de enseñanza como el Montessori, que se adapta muy bien a lo explicado anteriormente, ya que el niño desde las primeras edades comienza a combinar las representaciones manipulando objetos de la realidad en sus tres dimensiones y luego, asociándolos a las representaciones, mediante los símbolos conocidos como es el caso de las matemáticas.
Es bueno señalar que los autores del presente artículo, sin que constituyera específicamente un trabajo de tesis, visitaron en varias oportunidades un centro de este tipo en la ciudad de Lima, donde observaron las actividades realizadas desde los primeros, hasta los últimos años, y constataron el grado de independencia y poder creativo de los escolares durante las clases de Matemática.

Para ello se ofrecen las siguientes recomendaciones:
1) Orientaciones surgidas de la preparación de la clase con el fin de incluir los pasos previos para el modelo: a). Orientamos a los estudiantes a que traigan para la próxima clase varias varillas finas de madera o plástico como las que se usan para los conocidos anticuchos peruanos y b). También orientamos a que incluyan para esa clase un pequeño pedazo de plastilina.
2) En la clase: a). Los estudiantes tendrán listos, sobre cada mesa, los materiales. b). El docente (mediante plumón y regla, dibujará isométricamente un cubo en la pizarra), pero está utilizando un medio plano. Su objetivo es lograr que el alumno, observando la imagen, represente el objeto real en las tres dimensiones existentes, tal y como nos los ofrece la realidad concreta o la propia naturaleza.
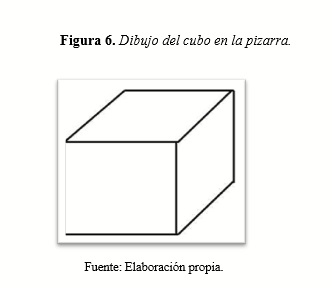
c). Luego ordenará que reproduzcan con los palitos y la plastilina esa figura geométrica que observaron en la pizarra (en este caso el cubo). Esto, generalmente, lo pueden hacer de forma individual y no está de más la consulta o el intercambio con sus compañeros de aula.
De esta forma estamos despertando el trabajo en equipo, contribuyendo a desarrollar valores de solidaridad. d). El estudiante reproducirá el dibujo representado en el plano, estereométricamente así:
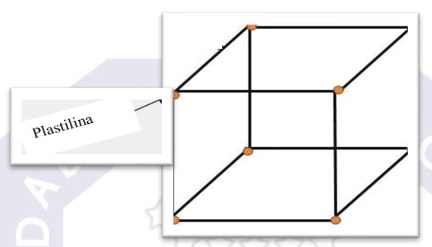
En este caso los estudiantes pueden hacer una reproducción de la figura observada en la pizarra, pero en tres dimensiones reales, donde acciona sobre el objeto, cuestión que permite adquirir mucha más información de la realidad. e). Según vaya avanzando en el sistema de clases, puede ejercer las mismas acciones con otras figuras geométricas de más complejas como son los casos de tetraedros, hexaedros, pirámides, etc. En estos casos, la visión plana cobra su información más completa en la mente del escolar cuando permite asimilarla en sus dimensiones reales, aparte del accionar a través de su tacto y llegar de forma tangible a la figura representada.
También, según la marcha del proceso, pueden hacerse preguntas más complejas sobre medidas de los ángulos dentro de cada figura, los lados y las proporciones entre ellos, lo cual completa el sistema de aprendizaje y se enriquecen las funciones didácticas durante el proceso educativo.
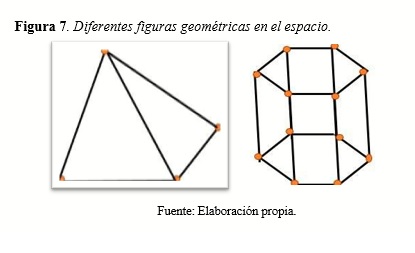
Si se estudian otras figuras que no poseen aristas definidas como por ejemplo el cono o el cilindro, el alumno se puede auxiliar de cartulina, tijeras y goma de pegar. El caso es que el propio estudiante accione sobre el objeto, y de esta forma, los conocimientos y habilidades tendrán más solidez y perdurarán por más tiempo en su mente.
En los ejemplos anteriores, el problema radica en conocer la forma real de las figuras para su futura aplicación práctica a través de un método de enseñanza que contribuye a desarrollar la creatividad mediante las capacidades de los escolares durante el estudio de la geometría del espacio.
Conclusiones
Como se ha expuesto en este trabajo, la enseñanza problémica forma parte de los métodos activos, y de una forma práctica, el docente puede poner en tensión las potencialidades del estudiante prescindiendo de aquellas formas de enseñanza que se divorciaban hasta cierto punto del aprendizaje por su carácter conductista. En los ejemplos anteriores, la contradicción estriba en partir de lo desconocido para llegar a conocer lo nuevo, actuando bajo la guía del docente, pero siempre teniendo en cuenta que los conocimientos antecedentes forman parte de la base conceptual y metodológica para lograr estadios superiores en el aprendizaje como, por ejemplo, cálculo de ángulos, de lados, proporciones en el espacio y problemas asociando varias figuras como las que construyó.
Como se observa en estos ejemplos didácticos, en la estereometría o geometría del espacio trabajados mediante este modelo de aprendizaje, la sugerencia aportada no necesita de costosos equipos ni de medios sofisticados si las clases se conciben de esta forma. Esta metodología responde a una solución que solo depende de la voluntad de los profesionales de la educación, por supuesto, los profesores.
Referencias
Álvarez de Zayas, C. (1981). La pedagogía como ciencia. La Habana.
Editorial Pueblo y Educación.
Área, M. (2004). Los medios y las tecnologías de la educación. Madrid: Pirámide.
Cabrera, J. C., Álvarez, A. y
Marrero, R. G. (2018). Enfoque problémico en los cursos para directivos del sector de justicia, Transformación, 14 (1), 58-69
Comenio, J. (1998). Didáctica magna. Octava edición. México:
Porrúa.
Del Valle, J, R. (1992). La Enseñanza Problémica y el laboratorio escolar. Holguín: ISPH.
García, S. (2015). Metodologías didácticas para la enseñanza y
aprendizaje de las ciencias naturales en zonas rurales
del municipio de Obando-Valle
del Cauca. (Tesis de maestría). Bogotá. Universidad Nacional de
Colombia. Recuperado el 17 de enero de 2017, de https://www.bdigital.unal.edu.co/
Godino, J y Ruiz, F. (2012). Geometría y su didáctica para maestros.
Universidad de Granada: ISBN: 84-932510-1-1
La Torre, M, Ariño, Seco, C,
J. (2016). Diseño Curricular para una
nueva sociedad. Lima: Editorial Santillana.
Majmutov, M. I.
(1983). La enseñanza problémica. La Habana: Pueblo
y Educación.
Montejo, M. N. (2016). La preparación
y edición de artículos científicos en el proceso de formación del investigador. Pedagogía
Universitaria, 21(1), 16-28. Recuperado de
https://cvi.mes.edu.cu/peduniv/index.php/peduniv/article/view/706
Nápoles C. Infantes, L. Quiles. Rivero M, y Ramírez,
R. (2004). Algunas consideraciones teóricas acerca de la Enseñanza Problémica. Rev. Hum Med v.4 n.1 Ciudad de Camagüey ene.-abr.
Ortiz, A. (2015). Metodología
para la enseñanza problémica de la contabilidad en la formación profesional. Méthodos, 13(13), 39-54 Recuperado de https://colmayorbolivar.edu.co/OpenJournalSys/index.php/Methodos/article/view/13
Palacio, J. (2003). Didáctica
de la Matemática: Búsqueda de Relaciones y contextualización de problemas. Lima: San Marcos.
Petrovski, A. V. (1984). Psicología General. Moscú: Progreso.
Piaget, J. (2013). Pensamiento concreto
y abstracto. Recuperado de https://prezi.com/7ufkrsisxqd/pensamiento-concreto-y-pensamiento-abstracto/
Reyes, C. C., Carrillo, S. E.
y Caamaño, R. M. (2017). Métodos problémicos e independencia cognoscitiva. Roca. Revista
científico-educacional, 13(2), 93-108
Román, M. (2005). Capacidades y valores como objetivos en la sociedad
del conocimiento. Santiago, Chile:
Arrayán.
Velarde, J. M. (2014). Modelo pedagógico problémico en el desarrollo de competencias argumentativas
en la educación secundaria. (Tesis doctoral). Universidad Nacional Pedro Ruiz Gallo. Lambayeque–Perú.
Vygotsky, L, S. (1987). Historia de las funciones
psíquicas superiores. La Habana: Científico Técnica.