Vocabulario matemático:
análisis del uso del sistema numérico en estudiantes adolescentes chilenos
Mathematical vocabulary: analysis of the use of the
numerical system in Chilean adolescent students
Autor corresponsal: anibal.puente@unab.cl.
https://orcid.org/0000-0003-3994-0553
Universidad Andrés Bello. Viña del Mar, Chile.
Ximena
González
ximenagonzalezvargas@gmail.com.
https://orcid.org/0000-0002-7836-3966
Universidad Andrés Bello. Viña del Mar, Chile.
Juan
Felipe Calderón
https://orcid.org/0000-0002-7248-4492
Universidad Andrés Bello. Viña del Mar, Chile.
DOI: https://doi.org/10.35756/educaumch.202118.203
Recibido:
3 de julio 2021
Evaluado: 20 de agosto 2021
Aceptado:
10 de diciembre 2021
Cómo citar
Puente, A., González, X. y Calderón, J. (2021). Vocabulario matemático: análisis del uso del sistema numérico en estudiantes adolescentes chilenos. Revista EDUCA UMCH (18), 36-57. https://doi.org/10.35756/educaumch.202118.203
Resumen
En el aprendizaje de las matemáticas, el léxico oral y escrito
de los alumnos puede informar
de algunos conceptos y su
forma de representación mental. Este es uno de los objetivos que se plantea en
este estudio. Para ello se implementó una prueba que aborda seis conceptos
matemáticos vinculados al sistema numérico y al valor posicional. La muestra incluyó
40 alumnos de Santiago de Chile de tres centros educativos (municipal, privado
subvencionado y privada) seleccionados de forma aleatoria, con rango de edad de
10 a 17 años. El análisis de los resultados evidenció la importancia del
vocabulario en contextos específicos para acceder a la disponibilidad léxica y
sus conceptos asociados. Esta línea de investigación permite estudiar las categorizaciones léxicas y ampliar
el campo de instrucción del vocabulario en la matemática. Una conclusión del estudio
es la enseñanza de las matemáticas como un lenguaje
y no como un mero
procedimiento.
Palabras clave:
vocabulario, matemática, léxico, conocimiento.
Summary
In the learning of
mathematics, students' oral and written vocabulary can inform about some concepts
and their form of mental representation. This is one of the objectives proposed
in this study. For this, a test was implemented that addresses six mathematical
concepts linked to the numerical system and positional value. The sample
included 40 students from Santiago Chile from three educational centers
(municipal, private subsidized and private) randomly selected, with an age
range of 10 to 17 years. The analysis of the results evidenced the importance
of vocabulary in specific contexts to access lexical availability and its
associated concepts. This line of research allows to study lexical
categorizations and expand the field of vocabulary instruction in mathematics.
One conclusion of the study is the teaching of mathematics as a language and not
as a mere procedure.
Key words: vocabulary, mathematics, lexicon, knowled.
Introducción
La enseñanza de las matemáticas es una política educacional que se ha institucionalizado en casi todas las culturas. En el Informe Cockcroft (1985) se considera que las matemáticas son útiles “porque proporcionan un método de comunicación que es poderoso, conciso y sin ambigüedades”. Sea porque diversos autores consideran este potencial comunicativo de las matemáticas, o bien por la representación simbólica que esta asignatura implica, han aparecido estudios que abordan el lenguaje matemático, específicamente desde su vocabulario (Hebert & Powell, 2016; Morgan, 2005; Monroe & Orme, 2002; Monroe & Pendergrass, 1997).
La relación existente entre lenguaje y vocabulario suele darse por entendida, en la medida que todo sistema de lengua mantiene elementos léxicos, sintácticos y semánticos que confluyen de formas creativas en diversos idiomas y dialectos. Y, como sabemos, las matemáticas presentan aspectos que implicarían la enseñanza de esta asignatura como una segunda lengua o, al menos, entendiéndola como una forma de desarrollar pensamiento y aprendizaje diferente (Nunes, 1999), esto por ser un sistema de representación con símbolos y sintaxis propia.
En el currículum educativo chileno, la enseñanza de las matemáticas se inserta en un marco de desarrollo comunicativo que ha de implementarse en los colegios. Sin embargo, el estudio de Preiss et al. (2001) evidencia que la práctica docente en Chile se orienta a repetición de ejercicios y en pocas instancias los estudiantes pueden movilizar conocimientos y conceptos, estrechamente vinculados al uso de vocabulario. Por lo mismo, para promover la enseñanza del lenguaje matemático es preciso conocer las palabras que los estudiantes manejan, enseñanza del lenguaje matemático es preciso conocer las palabras que los estudiantes manejan, cómo las utilizan y en qué contextos.
La forma en la que el
vocabulario matemático y el aprendizaje de la disciplina convergen es por medio
del modelo de Beck et al. (2013) en el que se distinguen tres niveles de
vocabulario. Un primer nivel está asociado a palabras de uso cotidiano; el
segundo, a palabras específicas de un área que suelen tener aplicación a más de
un área del conocimiento; y un tercer nivel, que presenta léxico específico de
una disciplina. Según las autoras, el segundo nivel permite el acceso a nuevo
conocimiento en la medida que ya conocen algunas palabras específicas,
produciéndose el “Efecto Mateo” (Stanovich, 1986) a nivel de vocabulario.
Desde hace algunos años, los
estudios sobre el impacto del vocabulario en el aprendizaje han tomado diferentes enfoques. A pesar de la importancia del vocabulario en el proceso
de enseñanza-aprendizaje, quienes estudian el vocabulario matemático y sus alcances
son recientes y distantes del contexto latinoamericano
y chileno. Así que para promover la enseñanza del lenguaje matemático es preciso conocer las palabras que los
estudiantes manejan, cómo las utilizan
y en qué contextos (Nortes-Martínez & Nortes-Checa, 2017; Nolla de Celis et al. 2021).
En ese sentido, este
estudio se erige como un acercamiento al conocimiento de los estudiantes sobre
lenguaje matemático. Para esto, se trabajará con los contenidos vinculados al
sistema numérico (entero y decimal) y valor posicional, que son críticos para
el aprendizaje de los otros contenidos de la disciplina y que, a la vez, se
asumen como materia aprendida en los niveles más avanzados de enseñanza
(Riccomini et al. 2015).
Realizaremos una revisión de aquello que entendemos por lenguaje y
cultura matemática, de la relación entre vocabulario y aprendizaje, y de las
tipologías de vocabulario matemático en el conocimiento de valor posicional y sistema numérico. Luego,
daremos a conocer la metodología utilizada, explicando en detalle el
instrumento utilizado y presentaremos los resultados del análisis que busca establecer los tipos de vocabulario
matemático para buscar establecer los tipos de vocabulario
matemático para, finalmente, discutir sobre dichos resultados. Para ello, se plantean las siguientes preguntas
de investigación:
·
¿Qué tipo de vocabulario
matemático es utilizado por los estudiantes en los niveles conceptual y procedimental del aprendizaje?
·
¿Cuáles son los conceptos
discursivos en los que ocurre el uso de vocabulario matemático en sus distintos niveles, según el modelo de Beck et
al. (2013)?
·
¿Cuáles son las recurrencias del
vocabulario matemático en las implicancias en el aprendizaje de los
estudiantes?
Lenguaje matemático y aprendizaje
La escritura en la asignatura de matemáticas implicaba abordar tareas tradicionalmente vinculadas a las áreas humanistas y, en este contexto, la profesora Burns (1995) plantea que en sus primeros veinte años de ejercicio docente esta mezcla le era tan extraña “como unir aceite y agua”. Sin embargo, ella fue observando beneficios en la producción textual dentro de la asignatura:
Creo que la escritura en la clase de matemáticas tiene dos grandes beneficios. Apoya el aprendizaje de los estudiantes porque, al poner sus ideas en el papel, los niños deben organizar, clarificar y reflejar su pensamiento. Escribir también beneficia a los profesores porque los textos de los estudiantes son un recurso de evaluación invaluable. Su escritura es una ventana hacia su entendimiento, cómo ellos enfocan sus ideas, qué errores albergan, y cómo se sienten sobre sus descubrimientos (p. 40).
Esta declaración sobre la estrecha relación entre escritura y aprendizaje nos acerca a la idea estudiada desde la aparición de las ciencias cognitivas: el lenguaje es un proceso cognitivo en ejercicio constante, que potencia otros procesos cognitivos, tales como el aprendizaje (Vygotsky, 1981).
Haciendo uso del lenguaje es que aprendemos. Sin embargo, es necesario conocer la lengua para poder llegar a niveles de conocimientos más profundos, como los conceptos abstractos. Entonces, cabe preguntarnos qué pasa si esa lengua no se conoce o no se demuestra competencia en ella. Un error frecuente que se observa en el ámbito educativo señala que el desarrollo de la práctica docente se centra en la mecanización de procedimientos. El alumno sabrá resolver una división, multiplicación, ecuación, etcétera, pero desconocerá cómo plantear un problema, dónde se pueda hacer uso de estas operaciones; es decir, el alumno conoce el procedimiento, pero le cuesta trabajo solucionar los problemas que impliquen la aplicación de cualquier operación básica (Batanero et al., 2011).
Debido a que las matemáticas implican el manejo de una serie de conceptos para poder profundizar su aprendizaje y llegar a comprenderlos y dado que, además, presentan un sistema representacional propio (numérico y simbólico) es que se habla de lenguaje matemático. Respecto de este punto, es necesario aclarar que esto no implica que sea una lengua, en el sentido de idioma; sino que tiene características lingüísticas propias que implican ser aprendidas para manejar ese lenguaje. Por otro lado, son diversos los estudios que abordan el concepto de lenguaje matemático (Hebert & Powell, 2016; Morgan, 2005; Monroe & Orme, 2002; Nunes, 1999).
Este problema es crítico en las escuelas chilenas, pues fracasan en el logro de un adecuado aprendizaje de la matemática, y una de las causas es el escaso uso y comprensión del lenguaje matemático. ¿Cómo mejorar dicho lenguaje? En primer lugar, es necesario clarificar que no existe un gen como marcador biológico; por el contrario, la mejora dependerá de los maestros, padres y los propios niños (Silva & Rodríguez, 2010). Por lo mismo, es necesario entender al lenguaje matemático como un constructo cultural. En palabras de Nunes 1999, “las matemáticas son una práctica cultural, y por tanto precisan una concepción particular de la naturaleza de los significados matemáticos y de los axiomas, que ya existen en la comunidad académica” (p. 33). Desde este punto de vista, la forma lingüística que adoptan las matemáticas debiera transmitirse considerándolas como herramientas culturales que los estudiantes puedan aprender. Ello es coherente con la visión de Vygotsky (1981) sobre el aprendizaje primero ocurre en lo social (i.e., entre las mentes de los individuos) y luego en el individuo mismo. Esto implica que, en la instancia social, se hace uso de herramientas culturales de cada sociedad en la que están insertos los sujetos. Estas herramientas culturales tomarían forma de las prácticas de cada sociedad, pero también de los saberes acumulados de esa cultura.
Vocabulario
matemático y tipologías
Para caminar hacia una instrucción léxica que promueva el aprendizaje en grupos de estudiantes con una brecha significativa en su conocimiento de palabras, Beck et al. (2013) realizan una propuesta que permite acompañar sus procesos de aprendizaje. El caso del lenguaje matemático no es ajeno a esta realidad, es por ello por lo que se plantea una tipología de lenguaje matemático que permita identificar las palabras que conocen los estudiantes y a qué niveles de vocabulario pertenecen.
En el primer nivel se encontrarán las palabras más básicas, “aparecen típicamente en conversaciones orales, y los niños están expuestos a ellas con una frecuencia alta desde una edad temprana” (p. 9), estas palabras no necesitarían atención instruccional en la escuela, pues la mayoría de los estudiantes las conocen. El segundo nivel de Beck et al (2013) presenta palabras que fortalecen la madurez lingüística de los hablantes, y atraviesan diversos campos disciplinares, las que además “son características del texto escrito y son infrecuentes en conversaciones, lo que significa que los estudiantes suelen aprenderlas menos de forma independiente, comparadas con las del primer nivel” (p. 9).
Por otro lado, las palabras del tercer nivel exigen de contextos constreñidos y específicos para que los niños las usen; muchas de estas palabras representan un aprendizaje profundo de una disciplina, pero para muchos estudiantes no resultan de mucha utilidad.
En esa línea, un estudio que atiende a los contextos de uso de vocabulario matemático es el de Hebert y Powell (2016). En él se analizan las ocurrencias de léxico matemático en un ensayo donde estudiantes de cuarto grado deben corregir la resolución de un problema matemático que contiene errores en distintos momentos. Para realizar un análisis léxico, recurren a la categorización de Monroe y Panchyshyn (1995, como se cita en Hebert & Powell, 2016), quienes plantean cuatro categorías:
1. Técnico, con un significado solo aplicable en matemáticas.
2. Subtécnico, con
múltiples significados que cambian a través de áreas de contenido o dentro de las matemáticas.
3. General, cuyo uso
ocurre en el lenguaje diario.
4. Simbólico, en el que
los significados son representados por medio de numerales o símbolos (p. 1515).
En la aplicación de las categorías de Monroe y Panchyshyn (1995), Hebert y Powell (2016) analizan y clasifican las palabras del examen escrito por los estudiantes. En este sentido, no siempre se puede acceder al conocimiento real que tienen los estudiantes, desde la noción de disponibilidad léxica (como caudal de palabras utilizable en una situación comunicativa dada, López, 1995), al no plantear diversos contextos que permitan evidenciar el uso de palabras matemáticas. Sin embargo, otorgan un marco de referencia útil para estudios posteriores y permiten establecer comparaciones entre el tipo de palabras utilizadas por estudiantes a través de diversos contextos educativos alrededor de la disciplina.
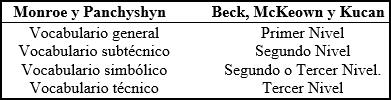
Al relacionar la categorización propuesta por Monroe y Panchyshyn (1995) con la categorización de Beck et al. (2013) es posible establecer ciertas analogías entre ellas (tabla 1). Es preciso mencionar que, si bien los niveles primero y tercero parecen coincidir sin grandes dificultades, en la relación entre el vocabulario subtécnico y el del segundo nivel hay que distinguir que no necesariamente se puede homologar la idea de que el conocimiento de léxico subtécnico permita una potenciación del desarrollo de aprendizaje, como sí lo consideran las palabras que entrarían en la categoría del segundo nivel en el modelo de Beck, McKeown y Kucan. De todos modos, es muy probable que una serie de palabras coincidan, siendo las matemáticas una base importante para diversos campos de las ciencias exactas. Por otro lado, cuando nos referimos al vocabulario simbólico, consideramos que pueden pertenecer tanto al segundo nivel como al tercero en la medida que el uso de numerales puede darse en diversos contextos, pero en el caso de algunos símbolos o abreviaturas matemáticas, solo ocurrirán en contextos disciplinares específicos (tales como fx, cos, ∑, √).
Tabla 1
Comparación entre los tipos de
vocabulario de las teorías de Monroe y Panchyshyn (1995, citados en Hebert & Powell, 2016) y de
Beck et al. (2013).
Metodología
Diseño: modalidad y enfoque
Con el fin de responder las preguntas de investigación previamente descritas se plantea en este trabajo una investigación de tipo explicativo no experimental (McMillan & Schumacher, 2005). Este estudio tiene características de una investigación cuantitativa, a partir de la exploración de asociaciones estadísticas entre las características de los sujetos participantes, su nivel de desempeño en la resolución y las categorías del vocabulario utilizado. Para obtener esta categorización, se utilizan herramientas propias de una investigación cualitativa, pues se realiza un análisis lingüístico de la estructura y el contexto del uso de conceptos matemáticos. Con ello se da pie a un enfoque metodológico mixto
Individuos
Los sujetos participantes de este estudio corresponden a 40 estudiantes de la ciudad de Santiago de Chile, pertenecientes a establecimientos educacionales de tres dependencias (municipal, privada subvencionada por el gobierno, y privada sin subvención). Los sujetos se escogieron de forma aleatoria y por conveniencia, considerando el rango de edad que va desde los 10 a los 17 años.
Instrumentos/medidas
Para analizar el vocabulario matemático que manejan los estudiantes, se implementó una prueba escrita que aborda seis conceptos matemáticos vinculados a sistema numérico y valor posicional, basado en los contenidos explorados desde quinto básico. Con el fin de acceder de manera adecuada al grado de conocimiento que los estudiantes tienen de los conceptos trabajados por esos contenidos, se establecen tres criterios que sintetizan las categorizaciones de Monroe y Panchyshyn (1995) y Beck et al. (2013, p. 1) se conoce el concepto si se usa operacionalmente al resolver un ejercicio o traspasar información verbal a numérica; 2) se conoce un concepto si se utiliza en un contexto que permite inferir el uso adecuado del término; y 3) se conoce un concepto si es explicado o definido por los estudiantes. Utilizando estas tres categorías se construye un instrumento que está estructurado en cinco secciones:
Sección I: representación simbólica de valor posicional
Esta sección tiene por finalidad establecer la comprensión de conceptos de valor posicional de los estudiantes. En la medida que saben posicionar los números solicitados dependiendo de su valor, entonces, existe conocimiento sobre los términos. Para ello, en la formulación de los ítems se solicita a los estudiantes la escritura de números enteros utilizando símbolos numéricos (i.e., dígitos del 0 al 9), a partir de la lectura de una cifra descrita por conceptos propios del valor posicional (e.g., “3 decenas, 5 unidades y 9 centenas”). En los ítems propuestos se intenta que el orden de la cifra a leer esté alterado, lo que implica un mayor grado de exigencia al momento de comprender la secuencia.
Sección II:
representación simbólica de sistema
numérico entero y decimal
En esta sección se
solicita a los estudiantes la escritura de una cifra dada utilizando símbolos numéricos, a partir de la lectura
de descripciones tales como “una milésima” o “una centena
de mil”. La comprensión del concepto se evidenciará a través del número escrito
por los estudiantes, similar al caso de los ítems de la sección I. No
obstante, en esta sección todos los números
solicitados en su valor posicional corresponden al dígito “1”. Con ello es
posible distinguir la existencia de diferencias entre la comprensión del valor posicional y la comprensión del sistema numérico.
Sección III: corrección
escrita sobre la resolución de un problema
matemático
A través de esta sección se busca que los estudiantes hagan uso de su vocabulario matemático para resolver un caso. El ejercicio consiste en corregir el error operacional cometido por un personaje denominado Paloma, quien se equivoca en la adición de dos cifras al no hacer coincidir las unidades y decenas de dos sumandos. En términos de acceso al conocimiento conceptual que tienen los estudiantes este ítem otorga un valor adicional a los anteriores, puesto que su uso aparece contextualizado en un caso verosímil. Ello permite el acceso a la disponibilidad léxica de los estudiantes desde el mismo instrumento, pues acota la situación comunicativa donde deben evidenciar el uso de vocabulario a una de carácter matemático.
Sección IV: uso de vocabulario del sistema numérico decimal en contexto
En línea con la anterior, en esta sección se promueve el uso contextualizado de conceptos matemáticos de sistema numérico decimal y valor posicional mediante la escritura de oraciones en las que los estudiantes deban usar palabras pertinentes al contexto, tales como “decena” o “milésima”. Para evitar la escritura de textos que limiten un análisis de vocabulario matemático, o bien un uso descontextualizado de las palabras, en los ítems propuestos se inicia cada oración con un pie forzado, el que los estudiantes deben completar.
Sección V: definición de conceptos
La última sección de este instrumento pretende analizar las definiciones realizadas por los estudiantes sobre términos trabajados anteriormente en la prueba. Por medio de preguntas como “¿Qué es una decena?” se busca explorar el conocimiento conceptual de los estudiantes sobre sistema numérico. La razón por la que este ítem se ubica al final de la prueba permite que los estudiantes ya hayan utilizado los conceptos por contextos o por resolución de problemas y no tengan que enfrentarse a una tarea epistemológicamente compleja, como la de definir, sin haberse enfrentado al uso de vocabulario pertinente al contexto matemático. Ello nos permite contrastar el uso correcto del término en los ítems anteriores con su correspondiente manejo conceptual evidenciado por la respuesta que ellos escriban.
El instrumento fue aplicado durante una hora pedagógica, correspondiente a 45 minutos y su extensión es de cuatro páginas, donde se incluyen 26 ejercicios que implican escribir cantidades con números, explicar con palabras conceptos matemáticos, completar oraciones utilizando palabras que indican conceptos de cantidad.
Análisis
El análisis de las respuestas obtenidas en las secciones I y II de la prueba consistió en establecer correspondencia entre las cifras dadas en el enunciado y las que los estudiantes respondieron de manera escrita. Para ello, se calificaron las respuestas de los estudiantes según corrección de su respuesta, asignando el valor 1 a las correctas y 0 a las incorrectas.
En el caso de la sección III, se
adaptó el método utilizado por Hebert y Powell (2016) de la rúbrica de la prueba de Composición de un Ensayo del Weschler Individual
Achievement Test – third edition (WIAT-III). En
este instrumento es donde se miden y analizan las ocurrencias de vocabulario matemático de acuerdo con
la tipología de Monroe y Panchyshyn (1995), adaptándolo para este estudio
utilizando las categorías del modelo de Beck
et al. (2013).
Las secciones IV y V servirán como apoyo para corroboración de datos y consistencia en los ítems anteriores. En el caso de la sección IV, la elaboración de oraciones escritas permite verificar el sentido de los conceptos utilizados dependiendo del contexto oracional, donde son claves las cargas semánticas de las palabras que rodean el término utilizado. Por último, la sección V será revisada evaluando la adecuación de uso de vocabulario matemático en la definición de conceptos mediante los tipos de definiciones que presentan y sus correcciones.
Finalmente, se realiza un análisis del uso de conceptos por parte de los estudiantes en las respuestas dadas en las secciones III, IV y V. Para ello se realizó un análisis descriptivo del uso léxico según el contexto oracional en el que los términos utilizados estén situados. Para ello, se utiliza un análisis experto por parte de tres lingüistas formados con el enfoque de gramática funcional de Dik et al. (1981). Posterior a ello, se revisará la consistencia entre el uso y definiciones de los conceptos a lo largo de las cinco secciones.
Resultados y discusión
Representaciones numéricas y variables
A través del análisis de la sección I, es posible apreciar la aplicación del conocimiento que tienen los estudiantes sobre valor posicional. Si bien la mayoría tuvo un buen resultado en el ejercicio, se evidenciaron dificultades en tres ítems que daban una cifra de más de un dígito a unidades, decenas, centenas o unidades de mil, como es el caso de los ítems (f), (h) y (j). A continuación, se presenta un ejemplo de respuesta para cada uno de los ítems mencionados, donde se aprecia la dificultad mencionada:
Enunciado del ítem: “Escribe con números las cantidades que se forman”: f) 12 decenas, 7 unidades y 8 centenas: 8129 (10 años) h) 10 centenas, 6 unidades de mil y 3 decenas: 6130 (16 años) j) 10 centenas, 12 unidades y 7 unidades de mil: 7112 (13 años).
Respecto de la edad de los sujetos, de manera intuitiva se aprecia una tendencia al aumento en el promedio de respuestas correctas en la medida en que su edad aumenta (figura 1). Ello no ocurre en los ítems (f), (h) y (j), los que ya han sido comentados.
Figura 1
Sección I: Promedio de respuestas correctas por item y
edad
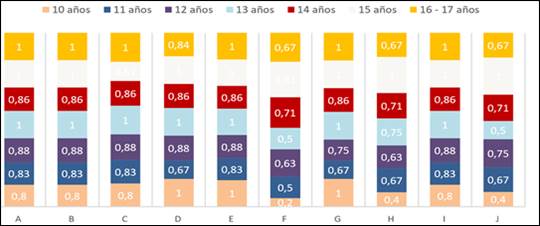
En el caso de la sección II, se buscaba indagar sobre el conocimiento de términos del sistema numérico decimal. Los estudiantes tuvieron éxito en la mayoría de las respuestas, sin embargo, presentaron mayores dificultades en las que respectan a la diferencia en términos propios de los números decimales, tal como es el caso de la pregunta por una milésima (ítem (a)) y por una décima (ítem (e)):
a) Una milésima: 1000 (14 años)
b) Una décima: 3 (15 años)
En el caso de la décima y milésima, los errores ocurridos en esta sección son consistentes con los de la sección IV, en la que los estudiantes escriben oraciones utilizando esos términos. De este modo, nos encontramos frecuentemente con el uso de “milésima” en el sentido de “unidad de mil” o “unidad de millón”, tal como en los siguientes casos que iniciaban con el pie forzado “La Mujer Maravilla”:
La Mujer Maravilla salvó
muchos gatitos, creo que era una milésima de gatitos. (10 años)
La Mujer Maravilla derrotó
a una milésima de malvados
con sus poderes. (12 años)
La Mujer Maravilla ha ayudado a milésimas de personas por la ciudad entera. (15 años)
En los tres ejemplos, los términos “muchos gatitos”, “malvados” y “personas” son elementos que nos permiten acceder a la creencia de que milésima es más que uno, incluso, es mucho más que uno, por la fuerza del plural de los sintagmas nominales y de complementos, tales como “con sus poderes” o “por la ciudad entera”. En cuanto a la edad de los participantes y sus respuestas, llama la atención que no hay un aumento significativo a medida que los estudiantes tienen una edad mayor, o al menos no hay un crecimiento sistemático del promedio en cuanto tienen más años, como se muestra en figura 2.
Figura 2
Sección
II: Promedio de respuestas correctas por item y edad
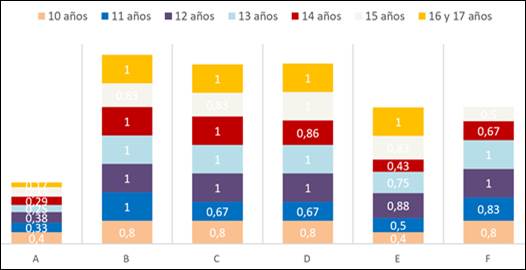
De este modo, se aprecia que los estudiantes tienen
manejo en valor posicional y sistema numérico, con algunos alcances en sistema
numérico decimal. Específicamente, los conceptos de milésima
y, en menor grado, décima. Aun así, esta base nos permite explorar si comunicacionalmente estos
conceptos son utilizados y en qué contextos. O bien, si en contextos verbales,
hay diferencias en el valor que se le da a cada concepto, como se mostró en los
ejemplos de la sección IV ya citados.
Uso
de vocabulario matemático
El problema presentado a los estudiantes en la sección III fue el siguiente:
III. Paloma estaba en clase de
matemática y su profesor le pidió que resolviera la siguiente operación: 105 +
39 =
Figura
3
Caso
1

Cabe destacar un manejo más alto de vocabulario en las mujeres más jóvenes versus los varones de esa misma edad (10 y 11 años), evidenciado en la cantidad de palabras utilizadas (tabla 2).
Tabla 2
Cantidad de palabras de vocabulario matemático
expresadas en la sección III según las variables
de sexo y edad.
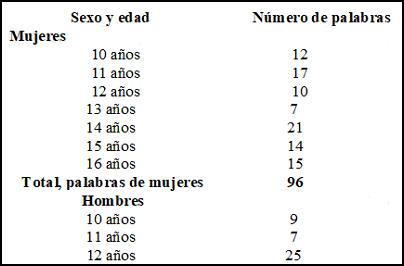
Tabla 3
Resultados caso hombres

En cuanto al tipo de palabras utilizadas, en la tabla 3 se muestran los 32 conceptos utilizados y su categorización en los niveles I, II y III de Beck, McKeown y Kucan (2013). La importancia que cobran numéricamente las palabras del nivel II, responden principalmente al contexto de la prueba y de la pregunta dada. Este nivel II nos permitió acceder a vocabulario que, probablemente, no habría aparecido en un contexto cotidiano. Ello se daría especialmente en aquellas de nivel III, que los estudiantes pueden conocer, pero no necesariamente utilizar en cualquier situación comunicativa, tal como indica Michéa (1953) sobre la disponibilidad léxica, explicada más arriba.
Tabla 4
Palabras utilizadas en sección 3 y categorización de
vocabulario en modelo de los tres niveles.
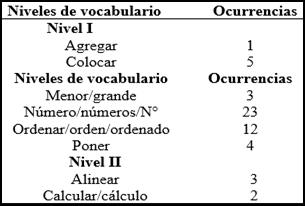
Tabla 5
Nivel de vocabulario

Como es posible
observar en la tabla III, las palabras
de nivel I aparecidas en los textos
escritos en esta sección de
la prueba se relacionan estrechamente con los valores posicionales de los sumandos, que es donde radica el error, de ahí que aparezcan términos
como “poner”, “colocar”, “ordenar”, que son más propios
del uso cotidiano a diferencia de “posicionar” o hablar de “valor posicional” que son palabras
vinculadas de forma más directa
con la disciplina. Obsérvense los siguientes ejemplos:
“Se equivocó en poner el número en la unidad
correcta, el profesor le dijo que
resolviera 105, pero ella se equivocó y puso el 105 en una unidad más grande, ya que debe ponerse el
número en su unidad correspondiente: 105.
+ 39
144”. (11 años)
“Paloma se equivocó
en cómo lo posicionó. Paloma
debería escribir la tabla de unidad, decena
y centena, separar
los números y ahí lo tendría ordenado
y podría sumar y obtener
un buen resultado”. (10 años).
En ambos casos, nos enfrentamos a un modo de organización
discursivo similar, identificando el problema
que tuvo Paloma al resolver el ejercicio y luego introducen la forma de solucionarlo con el verbo “deber”. Sin embargo, el
uso de vocabulario en ambos casos es diferente, en la medida que el nivel de especificidad del segundo es mayor al primero, utilizando términos como “posicionar”, “tabla de unidad, decena y
centena” y “resultado”, mientras que el primero, se plantea desde una perspectiva más coloquial al hablar de “poner
el número”, “unidad más grande” y
“unidad correspondiente”, sin especificar cuáles esta verbalmente, sino que lo
hace por medio del ejemplo de la
operación numérica. Esto también ocurre en la sección V al momento de
definir los conceptos de decena, unidad, centena,
décima y milésima.
Si bien en las secciones
anteriores es posible
evaluar el conocimiento que tienen los estudiantes al momento de utilizar los términos propios
de valor posicional y de sistema numérico, al
momento de definirlos suelen presentar algunos problemas con la
precisión del concepto. Por otro
lado, la estructura de la definición varía de uno a otro, como se puede
apreciar en los siguientes ejemplos
de respuestas frente a la primera pregunta de la sección: “¿Qué es una decena?”.
1.
10 (15 años)
2.
Una decena es un número natural del 0 al
9 que se ubica después de la unidad (12 años)
3.
Es una unidad multiplicada por 10 (13 años)
4.
El segundo dígito o 10 unidades
(12 años)
5.
Es una clasificación de los números
que van de 10 en 10 (10 años)
En los ejemplos dados, las formas de dar a conocer qué es una decena varían desde la sinonimia (respuestas 1, 3 y segunda parte de la 4), la remiten a su valor posicional (respuestas 2 y primera parte de la 5), o bien, la definen como un elemento que categoriza un conjunto numérico, en este caso, de múltiplos de 10 (respuesta 5). Esta variedad de respuestas refuerza la idea de Morgan (2005) sobre si los conceptos matemáticos tienen significados uno-a-uno entre palabra y representación. De alguna forma la variedad de definiciones o énfasis que se da a un concepto toma formas diversas dependiendo de qué están valorando más los estudiantes sobre ese concepto. De esta forma, se clasificaron los tipos de definiciones de los estudiantes a través de los siguientes tipos de definición (tabla 4).
Tabla 6
Tipos de definición utilizada
por los estudiantes en la sección V
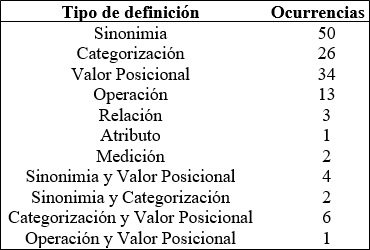
Es preciso mencionar que, en relación con las secciones anteriores, la sección V es de las que tiene un mayor porcentaje de error en sus respuestas, como se aprecia en la tabla 5.
Tabla 7
Errores y omisión de respuesta por ítem en la sección V
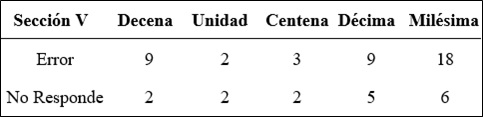
Debido a la mayor cantidad de errores al momento de definir, se evidencia que hay conceptos que los estudiantes saben aplicar, pero no necesariamente definir, mostrando las diferencias entre el conocimiento procedimental y el conceptual. Por otro lado, se refuerzan las dificultades presentadas en el aprendizaje del sistema numérico decimal, como se ha visto en las dos primeras secciones.
Discusión
Si asumimos que el lenguaje es el principal mediador del aprendizaje, no solo por ser una herramienta cultural básica para la transmisión de conocimientos, sino también porque es la que más se usa en el aula colectiva (Mercer y Littleton, 2016); entonces, podríamos asumir la importancia de enseñar el lenguaje. Esta idea suele tener fuerza en su primer enunciado, pero no necesariamente en el segundo, en especial, cuando se trata de disciplinas que no están directamente vinculadas a Lenguaje y Comunicación. Las matemáticas, así como las otras ciencias adoptan un nivel de conocimiento tan específico a lo largo de la vida escolar que se refleja en la especificidad del lenguaje que utilizan. La enseñanza, por tanto, del lenguaje de cada disciplina y de sus conceptos cobra vital importancia para el desarrollo del aprendizaje de los estudiantes en cada área (Beck et al., 2013; Nunes, 1999).
Es por la importancia de la enseñanza conceptual de las ciencias en general y de las matemáticas, en particular, que este estudio se propuso analizar el uso del vocabulario matemático en estudiantes de entre 10 y 17 años. Para ello, se identificó el conocimiento que tienen los estudiantes sobre lenguaje matemático por medio de su uso en representaciones numéricas y contextos discursivos variados, con el fin de identificar los tipos de vocabulario utilizados y establecer cómo la información levantada da luces sobre la forma en que se aprenden los conceptos matemáticos.
El análisis sobre representaciones numéricas de los términos de valor posicional y sistema numérico, abordados en las secciones I y II de la prueba, respectivamente, nos dieron luces sobre conceptos y modos de entrega de información que resultaban de mayor dificultad para los estudiantes. Esto ocurrió en momentos en que el valor asignado a una categoría posicional era de dos dígitos, dando como resultado múltiples errores y evidenciando un menor porcentaje de logro en mujeres. La segunda dificultad para los estudiantes se dio al momento de trabajar con sistema numérico decimal, frente a los conceptos de décima y milésima. Estos errores fueron consistentes con las pruebas verbales de los conceptos que aparecen en las secciones siguientes. Sobre este punto, cabe mencionar el énfasis que da Beck et al. (2013) sobre el tipo de palabras cuya instrucción debe ser reforzada, ya que es la que permite avanzar en una disciplina.
Debido a la importancia de la comprensión de conceptos matemáticos, consideramos fundamental
poder estudiar el manejo de los mismos términos de diferentes formas, de ahí
que se pregunte por sus representaciones numéricas,
su uso en oraciones, en la explicación de un problema y sus definiciones. En este sentido,
el concepto de disponibilidad léxica cobra importancia, ya que el proponer situaciones comunicativas que promuevan
el uso de léxico matemático fomentó
la utilización de conceptos que se vinculan, en las concepciones de los estudiantes, al sistema numérico y al
valor posicional. De esta manera, se puede acceder a la disponibilidad léxica de los estudiantes y evaluar el uso de
términos que de otra forma no aparecerían,
tales como “número de reserva”, “tabla de unidad, decena y centena”, “adición”
y “sumando”, entre otras. Esto, además, permite
establecer estrategias de instrucción sobre cómo se entiende cada concepto o cómo su acepción cambia
dependiendo de la operación o discusión que se tiene sobre la materia.
Junto a los elementos ya mencionados, fue posible apreciar que los estudiantes tienen mayor manejo en el conocimiento procedimental y de uso de vocabulario en contexto, antes que en las definiciones. La sección V puso en evidencia que como en nuestra lengua materna, el lenguaje matemático también es susceptible de diferentes interpretaciones dependiendo del contexto y modo en que se utilice. El hecho de que las definiciones dadas por los estudiantes reflejaran en su mayoría un uso o función del término (sinonimia y valor posicional), refuerza la idea de que el concepto en torno a una categoría de lo que implican las palabras de entrada, pueden estar más fuertemente atadas a una noción meramente conceptual y de poca aplicación en la asignatura. Así, es más útil para el estudiante decir que una decena puede indicar el valor posicional de una cifra o puede aludir a 10 unidades, en vez de indicar que es un término que se utiliza para designar un conjunto compuesto por diez elementos. Esto refuerza la interrogante de Morgan (2005) sobre cómo se definen los conceptos en las matemáticas que aparentemente son unidireccionales y libres de ambigüedad.
Los hallazgos descritos a través de este estudio permiten continuar dando fuerza a la importancia de seguir hablando de lenguaje matemático y nos impulsa a comprender que, si es un lenguaje, implica una cultura y actitudes que deben ser aprendidos, tal como lo señala Nunes (1999):
Aprender matemáticas en el aula es un proceso de socialización de antiguos significados en nuevos conceptos
característicos de las prácticas matemáticas.
Este proceso involucra reformar
o redescribir porque no es una simple inscripción de nuevos significados en conceptos antiguos. Las elecciones hechas
por los profesores para guiar el proceso de socialización
en el aula tienen un impacto en las redescripciones
que son hechas hacia un punto en el tiempo durante el proceso de aprendizaje (p. 40).
Como se aprecia en la cita, Nunes refuerza la noción de socializar en un aula colectiva los conceptos matemáticos, entendiendo que la mediación realizada por los docentes cobra vital importancia sobre el enfoque que se dará al concepto, coincidiendo con las conclusiones a las que llegan Beck, McKeown y Kucan (2013) y Morgan (2005). La tarea que queda, entonces, es promover una enseñanza consciente de los conceptos matemáticos de modo que su conceptualización se vea reforzada por su capacidad operacional y, así, reforzar el proceso de aprendizaje.
Conclusiones
Existen estudios sobre
el uso de vocabulario matemático en estudiantes de edad escolar,
siendo el más significativo,
el trabajo realizado por Hebert y Powell (2016) y otros más recientes (Powell, 2017; Powell, Hebert, Cohen, Casa
y Firmender, 2017). Así también, Morgan (2005)
ha estudiado el uso del vocabulario en textos escolares y otros
estudiosos lo han hecho desde los diccionarios. El problema que presentan estas investigaciones radica principalmente en que su análisis mide las entradas léxicas
desde sí mismas o con sus acepciones directas, sin considerar que el uso del vocabulario siempre será mediado
por un contexto (Dik, Valverde y
Mingorance, 1981) y es en él en donde toma diferentes énfasis y significaciones
las palabras.
De ahí que la presente investigación cobre importancia al explorar los mismos términos matemáticos desde entradas
y contextos diversos,
evaluando la consistencia o no del conocimiento que los alumnos tienen sobre sistema numérico
y valor posicional.
Retomando las preguntas de investigación propuestas en este estudio, en particular las relacionadas con la categorización del vocabulario utilizado por los estudiantes, se observa que es posible relacionar el tipo de términos que median el aprendizaje matemático respecto a valor posicional y sistema numérico, con la correcta comprensión de los mismos. El contar con esta información permite promover la instrucción específica de las entradas léxicas que no están siendo correctamente aprendidas, planteando el desafío de seguir estudiando las categorías de palabras utilizadas en otros contenidos matemáticos. Tal como se observó en los resultados existe distinto grado de corrección y tipo de vocabulario utilizado dependiendo de la edad. Ello se podrá corroborar con estudios cuantitativos futuros donde se explore la significancia de las correlaciones entre edad y tipo de vocabulario disciplinar, considerando el amplio rango de edades de los sujetos participantes del estudio (10 a 17 años).
Finalmente, llevando el análisis lingüístico realizado a un ámbito transversal del aprendizaje de distintas
disciplinas, se observa que de acuerdo con una revisión bibliográfica de los
teóricos Concha y Howard (2016) por
medio del análisis de diferentes estudios nacionales se muestra que:
Hay ciertas diferencias en las maneras de interactuar en el aula en las
distintas asignaturas. (…) En ese
sentido, una posible recomendación sería que cada curso de didáctica disciplinaria se hiciera cargo de enseñar las
interacciones verbales que favorecen su propio tipo de
pensamiento (p. 146).
De este modo, saber cuáles son las interacciones y conceptos que favorecen
el aprendizaje propio de cada disciplina es crítico para la promoción de
un aprendizaje significativo en el aula y poder acortar la brecha
existente entre el logro alcanzado entre hombres y mujeres en la disciplina,
dado que, como se mostró en esta investigación, a nivel de uso de vocabulario
las diferencias de género no son tan significativas como en los ejercicios y operaciones. Comprender la importancia de enseñar las
matemáticas como un lenguaje, cuyos conceptos
sean enseñados con el
énfasis en que son enseñados los procedimientos, nos ayudará
a avanzar en el conocimiento de la disciplina por parte de nuestros
estudiantes.
APF: Autor principal del artículo,
encargado de la idea original, la revisión bibliográfica, organización,
recogida de datos y diseño de instrumentos.
XG: Encargada en el
desarrollo de la metodología y resultados de la investigación.
JFC: Participación en el desarrollo de los resultados,
discusión, conclusiones de la investigación, revisión y edición de la
investigación.
Conflicto de intereses
Los autores declaran que no tienen
ningún tipo de conflicto de intereses en el desarrollo de su investigación.
Responsabilidades éticas o legales
Los participantes, en esta investigación, dieron su consentimiento para
el tratamiento de los datos requeridos; asimismo, se les informó sobre los
fines académicos de la información.
Declaración sobre
el uso de LLM (Large Language Model)
Este artículo de
investigación no ha utilizado para su redacción textos provenientes de LLM (ChatGPT u otros)
Financiamiento
La investigación se realizó con
los recursos propios de los autores.
Agradecimiento
A la región
Metropolitana de Santiago de Chile y a las comunas de Valparaíso y de Viña del
Mar.
Correspondencia: anibal.puente@unab.cl.
Referencias
Beck, I, L.,
McKeown, M., & Kucan, L. (2013). Bringing
words to life. Robust vocabulary instruction, Second Edition. https://www.guilford.com/beck-Studyguide.
Batanero, C. et al. (2011). Aprendizaje y
enseñanza de las matemáticas escolares: casos y perspectivas. Cuauhtémoc:
Secretaría de Educación Pública. https://es.scribd.com/document/282389218/APRENDIZAJE-Y-ENSENANZA-DE-LAS-MATEMATICAS-ESCOLARES-pdf
Burns, M. (1995). Writing in maths? Absolutly! Instructor, 104 (7), pp. 40-47. https://libgen.is/book/index.php?md5=6D26DB5921E16D0329142BB61CC07295
Cockcroft, W. (1985). Las matemáticas sí
cuentan: informe Cockcroft. Madrid: Ministerio de Educación y Ciencia.
Concha,
S., & Howard,
S. (2016).
Interacciones verbales en el aula y desarrollo de pensamiento: análisis de la situación en nuestro país y
propuestas formativas. En Manzi, J. y García, M. (Eds.). Abriendo las puertas
del aula. Transformación de las prácticas docentes. Santiago: Ediciones UC.
Dik, S., Valverde,
F. & Mingorance, L. (1981). Gramática
funcional. SGEL: Sociedad General Española de Librería.
Hebert, M., &
Powell, S. (2016). Examining fourth-grade mathematics writing: features of organization, mathematics vocabulary and
mathematical representations. Reading and Writing, 29(7), pp. 1511-1537. https://doi.org/10.1007/s11145-016-9649-5
López, H. (1995). Los estudios de disponibilidad léxica: pasado
y presente. Boletín de Filología 35,
pp. 245-259. https://revistapsicologia.uchile.cl/index.php/BDF/-article/view/19231/20354
McMillan, J., &
Schumacher, S. (2005). Investigación educativa
una introducción conceptual Madrid: Pearson educación.
Mercer, N., & Littleton, K. (2016). ¿Cómo
promueve la interacción el aprendizaje y el desarrollo? En Manzi, J. y García,
M. (Eds.). Abriendo las puertas del aula. Transformación de las prácticas
docentes. Santiago: Ediciones UC.
Michéa, R. (1953).
Mots fréquents et mots disponibles. Un aspect nouveau de la statistique du langage. Les langues modernes 47, pp. 338-344.
Morgan, C. (2005). Word, definitions and concepts in discourses of mathematics, teaching
and learning. Language and education, 19 (2), pp.
102-116. https://doi.org/10.1080/09500780508668666
Monroe, E., & Orme, M. (2002).
"Developing mathematical vocabulary." Preventing school
failure: alternative education for
children and youth, 46(3), pp. 139-142. https://doi.org/10.1080/10459880209603359
Monroe, E., &
Panchyshyn, R. (1995). Vocabulary considerations for teaching mathematics. Childhood Education, 72, pp. 80–83.
https://doi.org/10.1080/00094056.1996.10521849.
Monroe, E. E.,
& Pendergrass, M. R. (1997).
"Effects of mathematical vocabulary instruction on fourth grade students." Reading Improvement, 34, pp. 120–132.
Nolla de Celis,
A., Cerisola, A. Fernández, B., & Muñoz R. (2021).
Formación Inicial de los maestros en matemáticas y su didáctica. Revista Interuniversitaria de Formación del![]() Profesorado (RIFOR), 96 (35.1), 185-208. https://doi.org/10.47553/rifop.v96i35.1.85882
Profesorado (RIFOR), 96 (35.1), 185-208. https://doi.org/10.47553/rifop.v96i35.1.85882
Nortes, A., & Martínez-Artero, R. (2017).
Competencia matemática, actitud y ansiedad hacia
las Matemáticas en futuros maestros. Revista Electrónica Interuniversitaria de Formación del Profesorado (REIFOP), 20(3), 145-160. https://doi.org/10.6018/reifop.20.3.290841
Nunes, T. (1999).
Mathematics learning as the socialization of the mind.Mind, Culture and Activity, 6, pp. 33-52.
https://doi.org/10.1080/10749039909524712
Powell, S. (2017). An analysis of mathematical vocabulary from
kindergarten through eighth grades. (Manuscrito).
Powell, S. R., Hebert,
M. A., Cohen, J. A. Casa, T. M., & Firmender, J. M. (2017).
A synthesis of mathematics writing: Assessments,
interventions, and surveys.Journal of Writing
Research, 8(3), pp. 493-526.
Preiss, D., Larraín, A., &
Valenzuela, S. (2011). Discurso y
pensamiento en aula matemática chilena.
Psykhe 10(2), pp. 131-146. http://dx.doi.org/10.4067/S0718-22282011000200011
Riccomini, P. J.,
Smith, G. W., Hughes, E. M., & Fries, K. M. (2015). The language of mathematics: The importance of teaching and learning mathematical vocabulary. Reading and Writing Quarterly, 31(3), pp. 235-252.
Silva, M., & Rodríguez, A. (2010). ¿Por qué fallan los alumnos
al resolver problemas
matemáticos? Didac, 56, pp. 21-28.
Stanovich, K. (1986). Matthew
Effects in reading:
Some consequences of individual
differences in the acquisition of literacy. Reading Research
Quarterly, 21, pp. 360-407.
Vygotsky, L. S. (1981). Pensamiento y palabra. Infancia y Aprendizaje, 4(1), pp. 15-35. https://doi.org/10.1080/02103702.1981.10821886
Trayectoria académica
Aníbal Puente Ferreras
Doctor en Educación y
Sociedad, Magíster en Comprensión Lectora y Producción de Textos.
Actualmente ejerce la cátedra de Psicología Básica y ha escrito 15 libros, la
mayoría de ellos relacionados con procesos cognitivos y aprendizaje. También ha
participado en proyectos de investigación financiados y ha publicado artículos
en revistas científicas. Acompañan al doctor Puente, colaborando con algunos
capítulos, profesores de universidad con amplia trayectoria docente e
investigadora.
Ximena González
Licenciada en Lengua y
Literatura Hispánica, mención Lingüística en la Universidad de Chile. Profesora
de Castellano en Enseñanza Media en la Pontificia Universidad Católica de
Chile. Magíster en Comprensión lectora y Producción de textos en la Universidad
Andrés Bello. Actualmente me desempeño como profesora en el establecimiento
Cambridge College Antonio Varas en Chile, lugar en el que he desarrollado la
escritura de textos académicos con estudiantes de enseñanza media.
Juan Felipe Calderón
Profesor Asociado en
Universidad Andrés Bello. Doctor en Ciencias de la Ingeniería, Magister e
Ingeniero Civil en Computación de la PUC – Chile. Académico regular de la
Universidad Andrés Bello, sede Viña del Mar, desde el año 2014. Soy parte de la
Unidad de Innovación Docente y Académica (UNIDA), encargada de desarrollar la
línea de investigación e innovación educativa en ingeniería en nuestra
facultad.
Desarrollo sus actividades docentes de pre y postgrado en las áreas de ingeniería de software básica y aplicada a sistemas inteligentes, arquitectura de sistemas y cloud computing. Mis actividades de investigación las desarrollo en las áreas de diseño para el aprendizaje soportado por tecnología, innovación en educación en ingeniería, sustentabilidad en cloud computing e infraestructura tecnológica. En este momento estoy desarrollando dos proyectos financiados por ANID (como investigador principal y como coinvestigador), tanto de investigación básica como aplicada.
